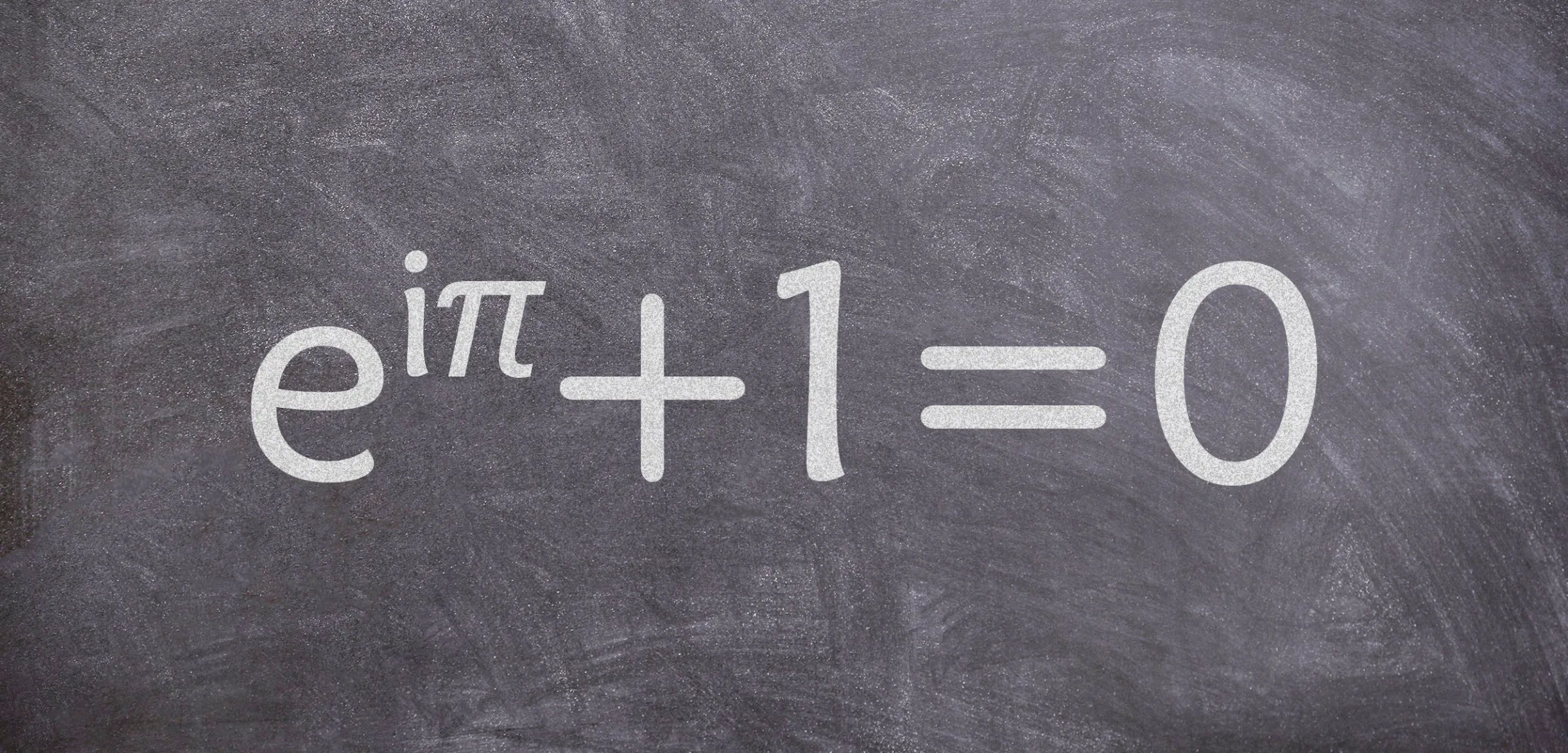
e wie Euler
Wäre die Schule einfacher ohne ihn? Bestimmt. Würde das Leben dadurch leichter? Auf keinen Fall. Leonhard Eulers Denken prägt das Leben bis heute.
«Sehr geehrter Herr Professor Euler. In Königsberg stehen sieben Brücken, welche die beiden Ufer des Pregel und zwei Inseln im Fluss miteinander verbinden. Ist es möglich, auf einem Spaziergang jede dieser Brücken zu überqueren, ohne eine zweimal zu betreten?» So ungefähr könnte der Brief gelautet haben, der Leonhard Euler 1736 erreichte.
Euler war 1707 in Basel geboren und in Riehen aufgewachsen. Von dort spazierte der Sohn eines Pfarrers bald täglich an die Universität, wo er im Alter von 13 Jahren sein Studium begann. Am meisten interessierte er sich für Mathematik und zu Eulers Glück lebte in Basel eine eigentliche Dynastie von Mathematikern: die Familie Bernoulli. Der junge Leonhard besuchte Johann und Jakob Bernoulli regelmässig. Die beiden förderten das junge Genie nach Kräften und als der 20-Jährige in Basel keine Professur erhielt, berief ihn Daniel Bernoulli kurzerhand zu sich nach St. Petersburg. Dort blieb Euler, bis es ihn 1741 nach Berlin verschlug, von wo ihn Katharina die Grosse 1766 wieder nach Russland holte.
Euler verfasste rund zwei Dutzend Bücher und über 800 Artikel, darunter solche zu Astronomie, Mechanik, Hydrodynamik, Hydraulik oder Musiktheorie. Seine grösste Leidenschaft aber blieb die Mathematik. Hier führte er eine ganze Serie neuer Zeichen ein, beispielsweise e, π, i, ∑ oder f(x). Aber Euler war kein trockener Theoretiker. Als er 1738 auf einem Auge erblindete, befasste er sich mit der Tränenflüssigkeit, stellte fest, dass ohne sie kein scharfes Sehen möglich ist, und verbesserte daraufhin Mikro- und Teleskope. Seine Erkenntnisse sind bis heute in jeder Fotokamera enthalten.

Druckgrafik aus dem 18. Jahrhundert mit einem Porträt von Leonhard Euler.
Schweizerisches Nationalmuseum
Eulers Denken war dynamisch und so befassen sich viele seiner Formeln mit Bewegung. Er hat Strömungen berechnet, sich mit dem Königsberger Spaziergang befasst und eine Formel dafür entwickelt, wie ein Springer über ein Schachbrett hüpfen muss, wenn er jedes Feld nur einmal betreten soll. Er stiess ins Reich der irrationalen Zahlen vor und seine «Eulersche Zahl» e erlaubt die Berechnung von Dingen, die sich permanent verändern. 1771 erblindete Euler auch auf dem zweiten Auge – und steigerte paradoxerweise daraufhin seine ohnehin schon rasante wissenschaftliche Produktion. Bereits 1748 stellte er überdies die Formel eiπ+1=0 auf und schuf damit – da sind sich die meisten Mathematiker einig – die schönste Formel ihres Fachs.
Übrigens: Das Brückenproblem konnte auch Euler nicht lösen. Dafür zeigte er, dass es unlösbar war. Und die Frage inspirierte ihn zu Formeln, die heute beispielsweise verwendet werden, um den effizientesten Fahrplan zu bestimmen. Oder den kürzesten Weg von A nach B. Oder auf welchem Weg die Müllabfuhr am besten durch eine Stadt fährt.

Titelblatt zu Euler «Vollständiger Anleitung zur Algebra» von 1771.
ETH-Bibliothek



